3 Graph Traversal
Graphs implement the interface Traversable, which has methods to get the predecessors and successors of a vertex and thus gives the opportunity to traverse a graph.This section will show some examples of graph algorithms using traversal.
3.1 Tarjan’s Strongly Connected Components
As a use case, the traversal package contains an implementation of Tarjan’s SCC algorithm, which divides a graph in its strongly connected components. A graph component is called strongly connected, if all pairs of vertices inside a component are reachable by each other.
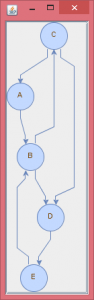
As an example we create a new graph and run Tarjan’s algorithm on it:
Graph<Integer> gt = new Graph<Integer>();
gt.addVertices(Arrays.asList("A", "B", "C", "D", "E", "F"));
gt.addEdge("A", "B"); gt.addEdge("B", "C"); gt.addEdge("C", "A");
gt.addEdge("D", "B"); gt.addEdge("D", "C"); gt.addEdge("D", "E");
a) b)
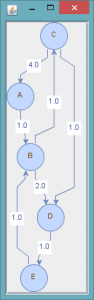
Figure 1: Visualization of an instance of the Graph class and an instance of the
WeightedGraph class.
gt.addEdge("E", "D"); gt.addEdge("E", "F"); gt.addEdge/"F", "C");
SCCTarjan tarjan = new SCCTarjan();
System.out.println(tarjan.execute(g));
The method getStronglyConnectedComponents() in the class TraversalUtils also uses this algorithm. It results in the following three components:
[[A, B, C], [D, E], [F]]
3.2 Custom Algorithm Using Traversal: Weakly Connected Graph
Besides using existing algorithms, it is also possible to use the Traversal interface to define custom algorithms. In this example, we want to know whether a given graph is weakly connected. A directed graph is called weakly connected if all pairs of edges are connected ignoring the direction of an edge.
The property can be retrieved in linear time by checking if all vertices are reachable over a weak connection from one random vertex. For this, we need a method, which recursively traverses all neighbours of a node. Neighbours can be retrieved by merging children and parents of a vertex. Vertices which are reachable from the starting vertex are stored in a set nodes.
private static <V extends Object> void weakConnectivityRec(
Traversable<V> graph, V v, Set<V> nodes) {
Set<V> neighbours = new HashSet<V>();
neighbours.addAll(graph.getChildren(v));
neighbours.addAll(graph.getParents(v));
for (V n : neighbours) {
if (false == nodes.contains(n)) {
nodes.add(n);
weakConnectivityRec(graph, n, nodes)
}
}
}
The algorithm collects all weakly connected vertices from an arbitrary vertex. A graph is weakly connected, if the set of weakly connected vertices is as large as the set of vertices in the graph. Since the set of connected nodes also contains the start node, we just test if this set is smaller than the set of all vertices.
public static <V extends Object> boolean isWeaklyConnected(
Traversable<V> graph) {
for (V node : graph.getNodes()) {
Set<V> nodes = new HashSet<V>();
weakConnectivityRec(graph, node, nodes);
if (nodes.size() < graph.getNodes().size())
return false;
break;
}
return true;
}
Though this code snippet looks unnecessarily confusing, the outer loop, which gets interrupted after the first iteration, is needed to retrieve an element from a Collection data type.
The class TraversalUtils also contains methods to retrieve meta information of a graph and its components. To check if a graph is strongly connected, we can use the static method isStronglyConnected. Furthermore it’s worth to take a look at the method implementations in that class, since they are using the Traverser class, which already implements the depth-first-search and the breadth-first-search. As a consequence the implemented methods stay very compact.
A coloring of graphs assigns a color to each vertex, such that no neighboured vertices have the same color. Graph coloring algorithms try to get along with a minimum number of different colors. If a graph can be colored using k different colors, it is called a k-coloring graph. For example it is possible to color a world map with four different colors, such that no neighboured countries have the same color (Four color theorem).
The Coloring class represents a coloring of vertices. The class GraphColoringFactory has a method exactGreedyColoring to create a coloring for a graph.
Graph coloring can be used to determine whether a graph is bipartite i.e. it can be separated in two disjoint groups of vertices, which are not adjacent among themselves. In this case, there must be a coloring for the graph with only two different colors:
public static <V extends Object> boolean isBipartite(Graph<V> g) {
Coloring c = GraphColoringFactory.exactGreedyColoring(g);
return c.getColorGroups().size() == 2;
}
The following two graphs show examples of the algorithm. The left one is bipartite, since it can be colored using two colors, where The right graph needs three colors and therefore is not bipartite.
